LaunchPad35a
Mon blog personnel sur l'espace
LaunchPad35a

Comment lancer un relais de 3 Satellites en orbite géostationnaire ? (WIP)

Posted on

Pour pouvoir envoyer des messages facilement d’un bout à l’autre de la planète sans utiliser trop de ressources, le moyen le plus simple est de lancer un relais de trois satellites en orbite géostationnaire. Cela permet que les satellites soient toujours en contact entre eux et qu’ils puissent desservir toute la surface de la terre.

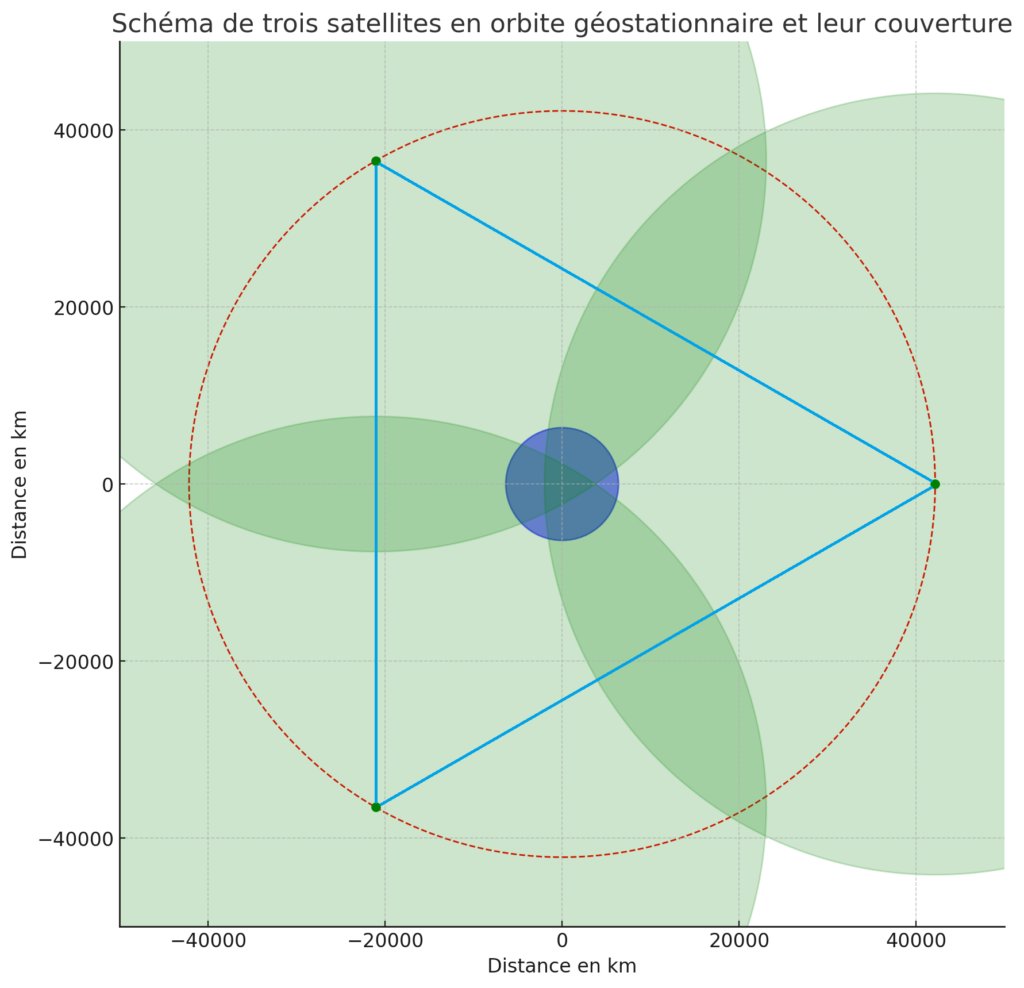
On peut voir sur ce schéma que l’entièreté de la surface de la Terre est couverte par les satellites
Étapes du voyage des satellites

Le voyage se fait en 4 étapes :

  1. L’envoi des satellites en orbite basse, à 400 km d’altitude.
  2. Orbite de transfert géostationnaire (GTO).
  3. Orbite « de livraison », qui permet de délivrer les satellites.
  4. Orbite Géostationnaire.
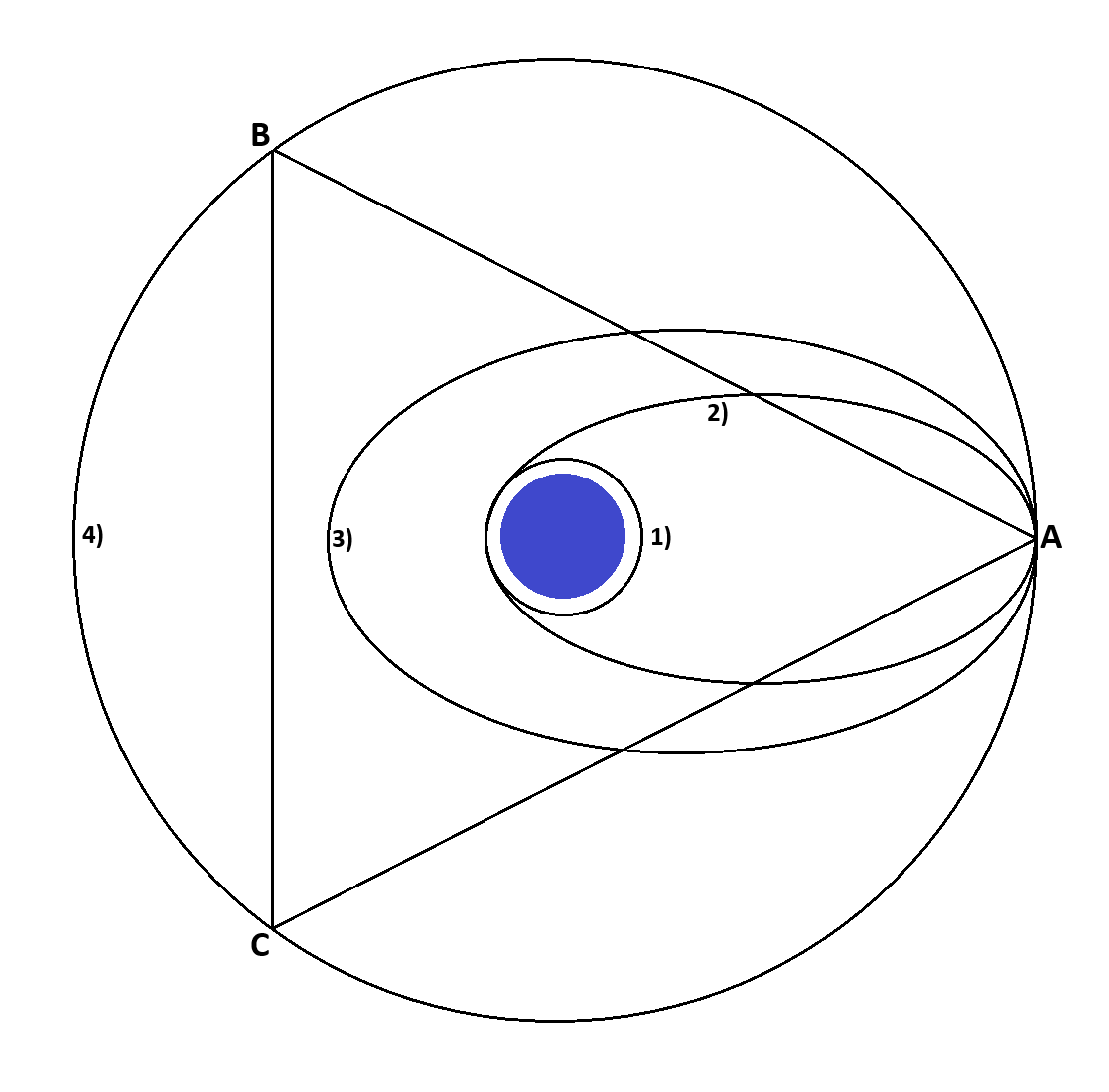
Schéma des orbites utilisées pour la mise en place de la

Rappels :

2ème loi de Newton :

\[ \mathbf{F} = \mathbf{a} \times m \]

3ème loi de Kepler :

\[ \frac{T^2}{r^3} = \text{constante} \]

Loi de l’attraction universelle :

\[ F = \frac{GM_{t}m}{r^2} \]

Energie potentielle de Gravitation :

\[ E_{pg} = -\frac{GM_{t}m}{r} \]

A partir de ces formules on peut en déduire 3 autres :

\[ v = \sqrt{\frac{GM}{r}} \] \[ E_{\text{mécanique}} = -\frac{G \cdot m \cdot M_{t}}{2 \cdot r} \] \[ r = \sqrt[3]{\left(\frac{T^{2}GM_{t}}{4\pi ^{2}}\right)} \]

Quelques données supplémentaires :

Étapes du voyage des satellites

Le voyage se fait en 4 étapes :

  1. Rayon de la Terre (Rt): 6.371 × 106 m
  2. Masse de la Terre (Mt): 5.972 × 1024 kg
  3. Constante gravitationnelle (G): 6.674 × 10-11 N·m2/kg2

Delta-V :

Le delta V est une valeur utilisée en aérospatiale pour connaitre la capacité d’un satellite, elle permet de remplacer l’énergie cinétique, qui est dépendante de la masse. Les calculs de Delta-V peuvent s’appliquer à n’importe quelle masse.

Nous allons donc calculer le delta-V nécessaire pour aller de l’orbite basse jusqu’à ce que tous les satellites soit placés au bon endroit. Pour cela il faut calculer de delta d’énergie entre chaque orbite.

1) Energie de l’orbite Basse

Résolution de l’énergie mécanique avec MathJax

La formule mécanique est donnée par :

\[ E_{\text{mécanique}} = -\frac{G \cdot m \cdot M_{t}}{2 \cdot r} \]

On sait que :

  • Rayon de la Terre (Rt): 6.371 × 106 m
  • Rayon de l’orbite (r = Rt + 400km): 6.771 × 106 m
  • Constante gravitationnelle (G): 6.674 × 10-11 N·m2/kg2
  • Masse de la Terre (Mt): 5.972 × 1024 kg
\[ E_{\text{mécanique}} = -\frac{6.674 \times 10^{-11} \times 1 \times 5.972 \times 10^{24}}{2 \times 6.771 \times 10^{6}} \] \[ E_{\text{mécanique}} = m \times(-2.9391 \times 10^{7}) \text{ joules} \]

On doit maintenant calculer l’énergie en orbite te transfert, pour cela on a besoin du demi-grand axe. on peut calculer ce demi-grand axe par la formule :

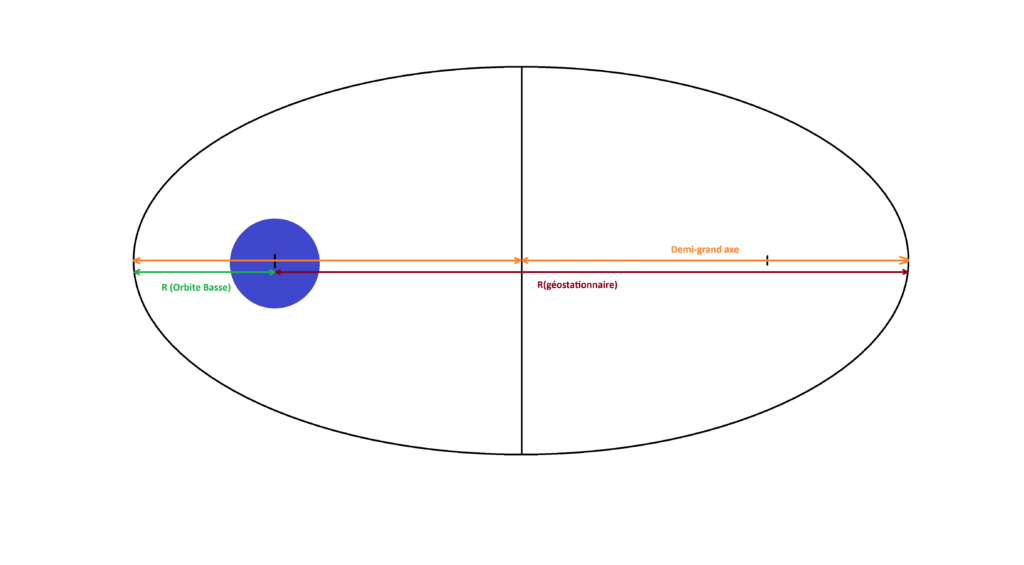
Résolution de l’énergie mécanique avec MathJax
\[ a = \frac{{(R_{\text{orbite basse}} + R_{\text{géostationnaire}})}}{2} \]

On a donc besoin de calculer le rayon de l’orbite Géostationnaire pour cela on utilise la formule :

Résolution de l’énergie mécanique avec MathJax
\[ r = \sqrt[3]{\left(\frac{T^{2}GM_{t}}{4\pi ^{2}}\right)} \ \]
Calcul du rayon de l’orbite géostationnaire avec MathJax

La période de révolution \( T \) est de 24 heures (86400 secondes).

\[ R_{\text{géostationnaire}} = \sqrt[3]{\left(\frac{(24 \times 3600)^{2} \cdot 6.674 \times 10^{-11} \cdot 5.972 \times 10^{24}}{4\pi ^{2}}\right)} \] \[ R_{\text{géostationnaire}} \approx 4.216 \times 10^7 \text{ m} \]

On peut donc déterminer le demi-grand axe :

Détermination du demi-grand axe avec MathJax

Le rayon de l’orbite basse \( R_{\text{orbite basse}} \) est \( 6.771 \times 10^6 \) m.

Le rayon de l’orbite géostationnaire \( R_{\text{géostationnaire}} \) est \( 4.216 \times 10^7 \) m.

\[ a = \frac{{(6.771 \times 10^6 + 4.216 \times 10^7)}}{2} \] \[ a = 2.44655 \times 10^7 \text{ m} \]

On peut donc calculer l’énergie mécanique de l’orbite de transfert:

Calcul de l’énergie mécanique d’une orbite géostationnaire avec MathJax

Calcul de l’énergie mécanique d’une orbite elliptique

A partir de la formule :

\[ E_{\text{mécanique(Orbite elliptique)}} = -\frac{G \cdot m \cdot M_{t}}{2 \cdot a} \] \[ E_{\text{mécanique(Orbite elliptique)}} = m \times(-\frac{6.674 \times 10^{-11} \times 5.972 \times 10^{24}}{2 \cdot 2.44655 \times 10^7}) \] \[ E_{\text{mécanique(Orbite elliptique)}} \approx m \times(-8.14 \times 10^6) \text{ joules} \]

Les satellite est maintenant sur l’orbite de transfert, mais ils ne peuvent pas accélérer jusqu’à l’orbite géostationnaire, car ils doivent être séparés par un certain intervalle. Les satellites doivent donc se placer sur une seconde orbite elliptique, que l’on va appeler « orbite de livraison ». Cette orbite a une période de révolution de 2/3 de l’orbite géostationnaire, soit 16h. Cette orbite va permettre que les satellites déjà lancé sur l’orbite géostationnaire parcourent 2/3 de celle-ci pendant que ceux restés sur l’orbite de livraison aient fait 1 tour et soient revenus au point de lancement.

Au premier tour, le satellite 1 est lancé en A
Au second tour, le premier satellite est placé en C, Le second satellite est lancé
Le premier satellite st en B, le second en C et le premier est lancé en A

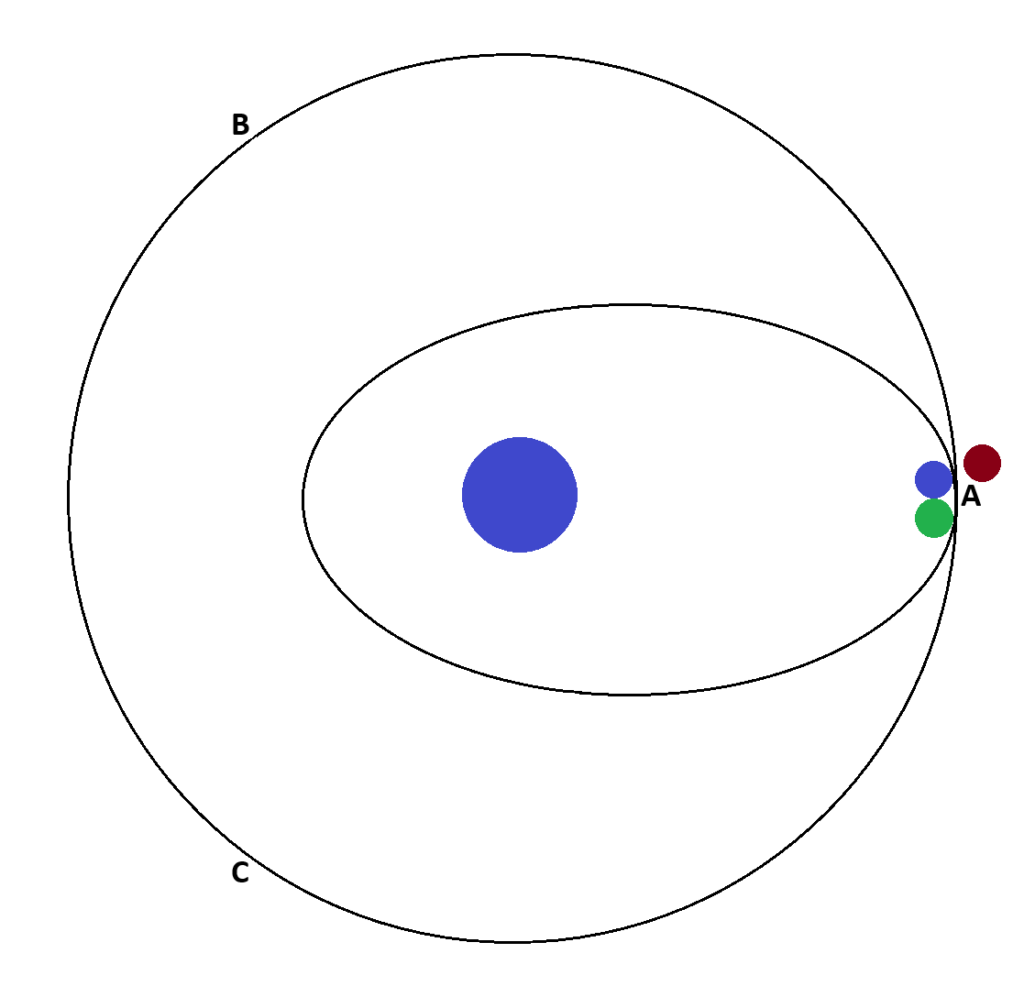
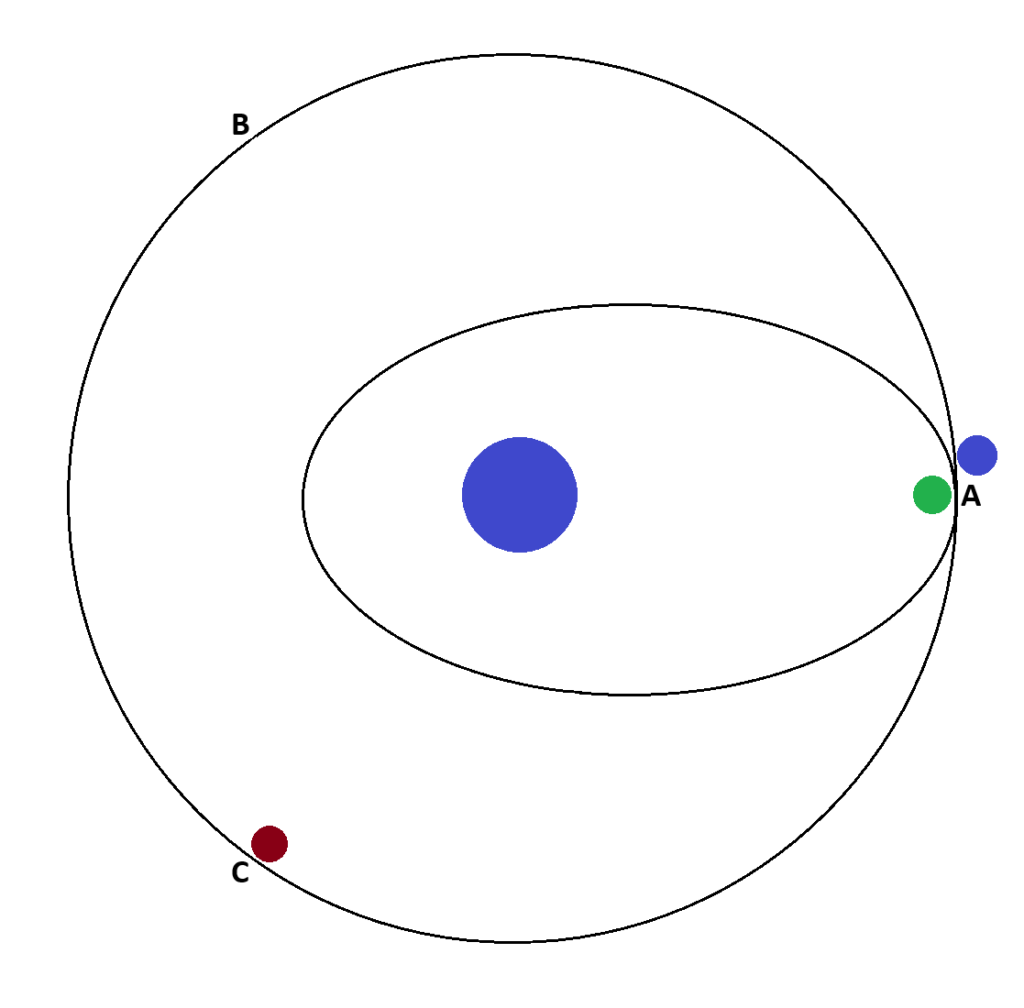
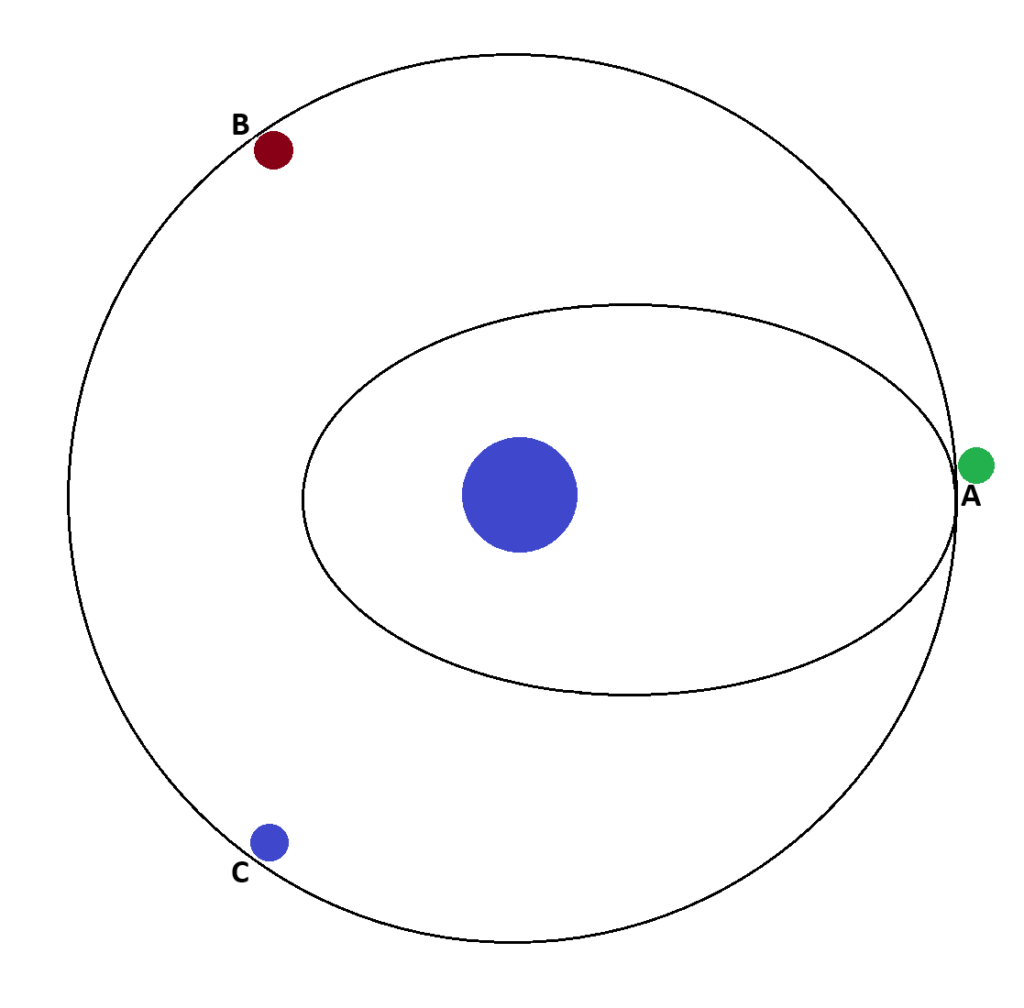
On cherche donc l’énergie de cette orbite. Pour cela on a besoin de calculer le demi-grand axe, que l’on va déterminer grâce à la Troisième loi de Kepler :

\[ \frac{T^2}{r^3} = \text{constante} \]

On détermine cette constante avec les paramètres orbitaux de l’orbite Géostationnaire

Calcul du demi-grand axe avec MathJax
  • La période de révolution \( T_{\text{orbite livraison}} \) est \( 57600 \) secondes.
\[ \frac{R_{\text{orbite géostationnaire}}^3}{T_{\text{orbite géostationnaire}}^2} = \frac{a_{\text{orbite livraison}}^3}{T_{\text{orbite livraison}}^2} \] \[ a_{\text{orbite livraison}} = \sqrt[3]{\frac{T_{\text{orbite livraison}}^2 \cdot R_{\text{orbite géostationnaire}}^3}{T_{\text{orbite géostationnaire}}^2}} \] \[ a_{\text{orbite livraison}} = \sqrt[3]{\frac{(57600)^2 \cdot (4.216 \times 10^7)^3}{(86400)^2}} \] \[ a_{\text{orbite livraison}} \approx 3.2205 \times 10^7 \text{ mètres} \]

On détermine maintenant l’énergie mécanique de l’orbite de livraison

Calcul de l’énergie mécanique avec MathJax
\[ E_{\text{mécanique}} = -\frac{G \cdot m \cdot M_t}{2 \cdot a_{\text{orbite livraison}}} \]

En insérant les valeurs on obtient :

\[ E_{\text{mécanique}} = -\frac{6.674 \times 10^{-11} \cdot m \cdot 5.972 \times 10^{24}}{2 \cdot 3.2205 \times 10^7} \]
\[ E_{\text{mécanique}} = -6.18 \times 10^6 \times m \text{ joules} \]

On calcule l’énergie de l’orbite Géostationnaire

Calcul de l’énergie mécanique avec MathJax
  • \( R_{\text{orbite géostationnaire}} = 4.216 \times 10^7 \) mètres.
\[ E_{\text{mécanique(Orbite géostationnaire)}} = -\frac{G \cdot m \cdot M_t}{2 \cdot R_{\text{orbite géostationnaire}}} \]
\[ E_{\text{mécanique(Orbite géostationnaire)}} = -\frac{6.674 \times 10^{-11} \cdot m \cdot 5.972 \times 10^{24}}{2 \cdot 4.216 \times 10^7} \] \[ E_{\text{mécanique(Orbite géostationnaire)}} \approx -4.727 \times 10^6 \times m \text{ joules} \]

On cherche maintenant le delta d’énergie entre chaque orbite

Calcul de la différence d’énergie mécanique avec MathJax

Les énergies mécaniques des orbites basses et de transfert :

  • Pour la première orbite : \( E_1 = -8.14 \times 10^7 \times m \) joules
  • Pour la deuxième orbite : \( E_2 = -2.9391 \times 10^7 \times m \) joules
\[ \Delta E_{\text{mécanique, basse/transfert}} = E_1 – E_2 \] \[ \Delta E_{\text{mécanique, basse/transfert}} = (-2.9391 \times 10^7 \times m) – (-8.14 \times 10^7 \times m) \] \[ \Delta E_{\text{mécanique, basse/transfert}} = 2.12 \times 10^7 \times m \text{ joules} \]
Calcul de la différence d’énergie mécanique avec MathJax

Les énergies mécaniques des orbites de transfert et de livraison :

  • Pour l’orbite de livraison : \( E_{\text{mécanique, livraison}} = -1.065 \times 10^7 \times m \) joules
  • Pour l’autre orbite : \( E_{\text{mécanique, transfert}} = -8.14 \times 10^7 \times m \) joules
\[ \Delta E = E_{\text{mécanique, livraison}} – E_{\text{mécanique, transfert}} \] \[ \Delta E_{\text{mécanique, transfert/livraison}} = (-6.18 \times 10^6 \times m) – (-8.14 \times 10^6 \times m) \] \[ \Delta E_{\text{mécanique, transfert/livraison}} = 1.96 \times 10^6 \times m \text{ joules} \]

Les énergies mécaniques des orbites de livraison et géostationnaire :

  • Pour l’orbite de livraison : \( E_{\text{mécanique, livraison}} = -1.065 \times 10^7 \times m \) joules
  • Pour l’orbite géostationnaire : \( E_{\text{mécanique, géostationnaire}} = -4.727 \times 10^6 \times m \) joules
\[ \Delta E = E_{\text{mécanique, géostationnaire}} – E_{\text{mécanique, livraison}} \] \[ \Delta E_{\text{mécanique, livraison/géostationnaire}} = (-4.727 \times 10^6 \times m) – (-6.18 \times 10^6 \times m) \] \[ \Delta E_{\text{mécanique, livraison/géostationnaire}} = 1.45 \times 10^6 \times m \text{ joules} \]

En considérant que l’énergie est fournie par l’énergie cinétique.

\[ \Delta E = \Delta E_{\text{cinétique}} \] \[ \Delta E_{\text{cinétique}} = \frac{m \cdot \Delta v^2}{2} \] \[ \Delta v = \sqrt\frac{2 \cdot \Delta E}{m} \]

On calcule les delta-V :

Pour aller de l’orbite basse à l’orbite géostationnaire :

\[ \Delta E = 2,12 \cdot 10^7 \] \[ \Delta v = \sqrt\frac{2 \cdot 2,12 \cdot 10^7 \cdot m}{m} \] \[ \Delta v = \cdot 10^7 \]

Laisser un commentaire